Binary Search Tree
Binary Tree
이진 트리는 하위 노드를 최대 2 개를 가지고 있는 트리를 말합니다.
Binary Seach Tree
이진 탐색 트리는 이진 트리에 몇 가지 조건이 추가 된 트리입니다.
- 노드의 왼쪽 하위 트리에는 자신보다 값이 작은 노드만 존재합니다.
- 노드의 오른쪽 하위 트리에는 자신보다 값이 큰 노드만 존재합니다.
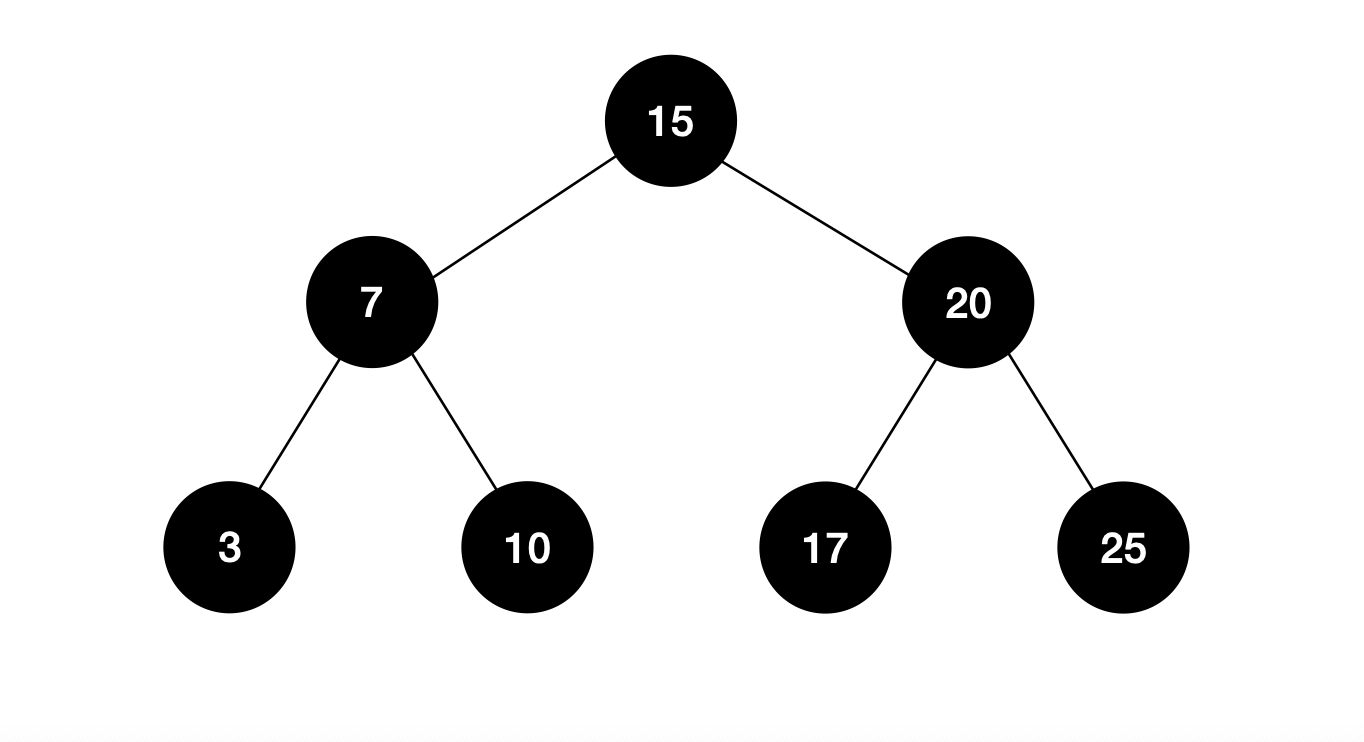
탐색
- 이진 탐색 트리는 정렬이 되어있다는 조건이 있기 때문에 쉽게 원하는 키를 탐색할 수 있습니다.
- 균형잡힌 트리라면 O(logN)의 시간이 걸리지만 위처럼 불균형하다면 O(N)의 시간이 걸릴 수 있어 최적화 과정이 필요할 수 있습니다.
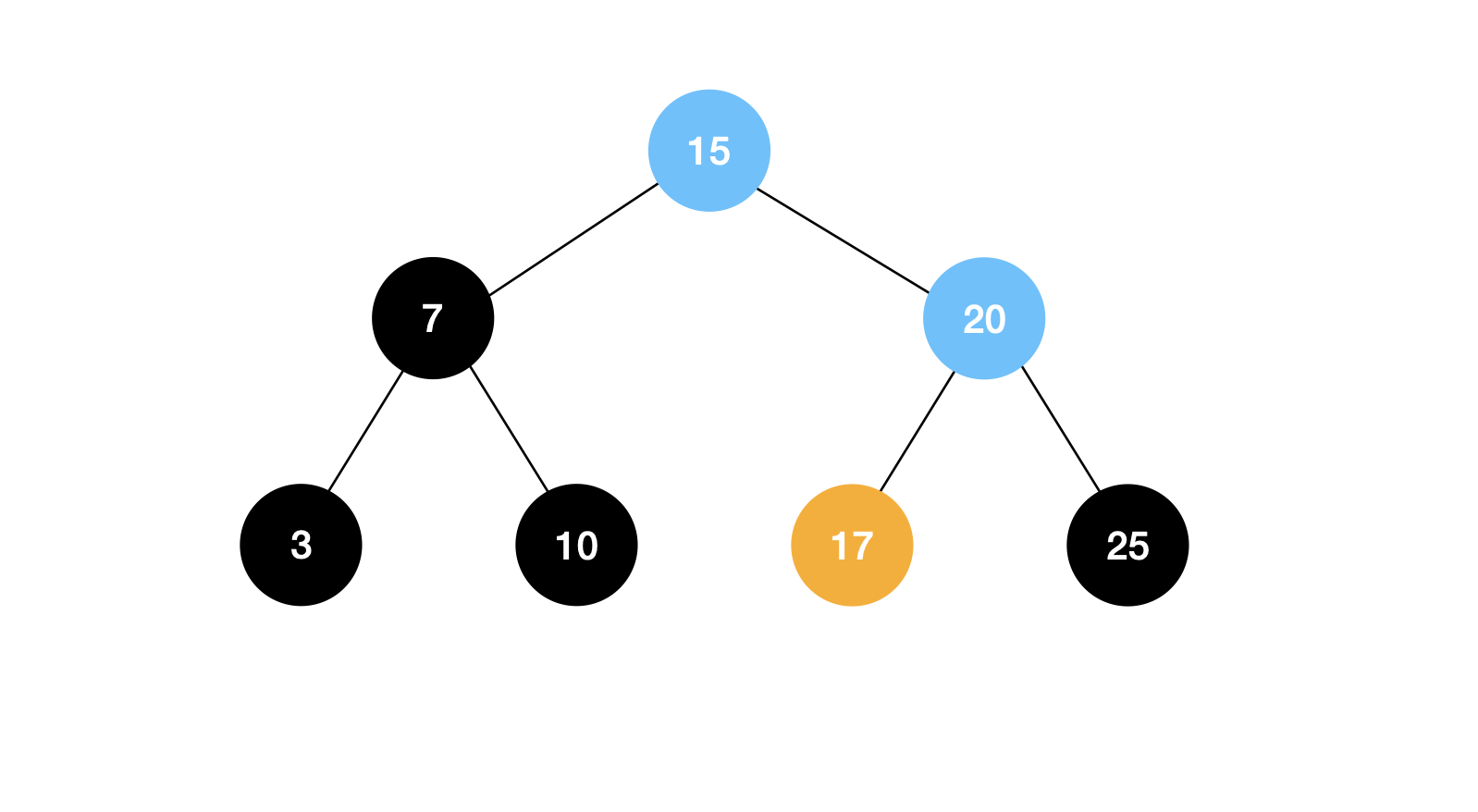
- 루트 노드의 key인 15와 탐색하길 원하는 key인 15와 크기를 비교 (15 < 17)
- 17이 15보다 크기 때문에 루트 노드의 오른쪽 하위 노드의 키를 비교 (20 > 17)
- 17이 20보다 작기 때문에 노드의 왼쪽 하위 노드의 key와 비교 (17 == 17)
- 노드의 key와 탐색 목표 key인 17이 같기 때문에 탐색 종료
삽입
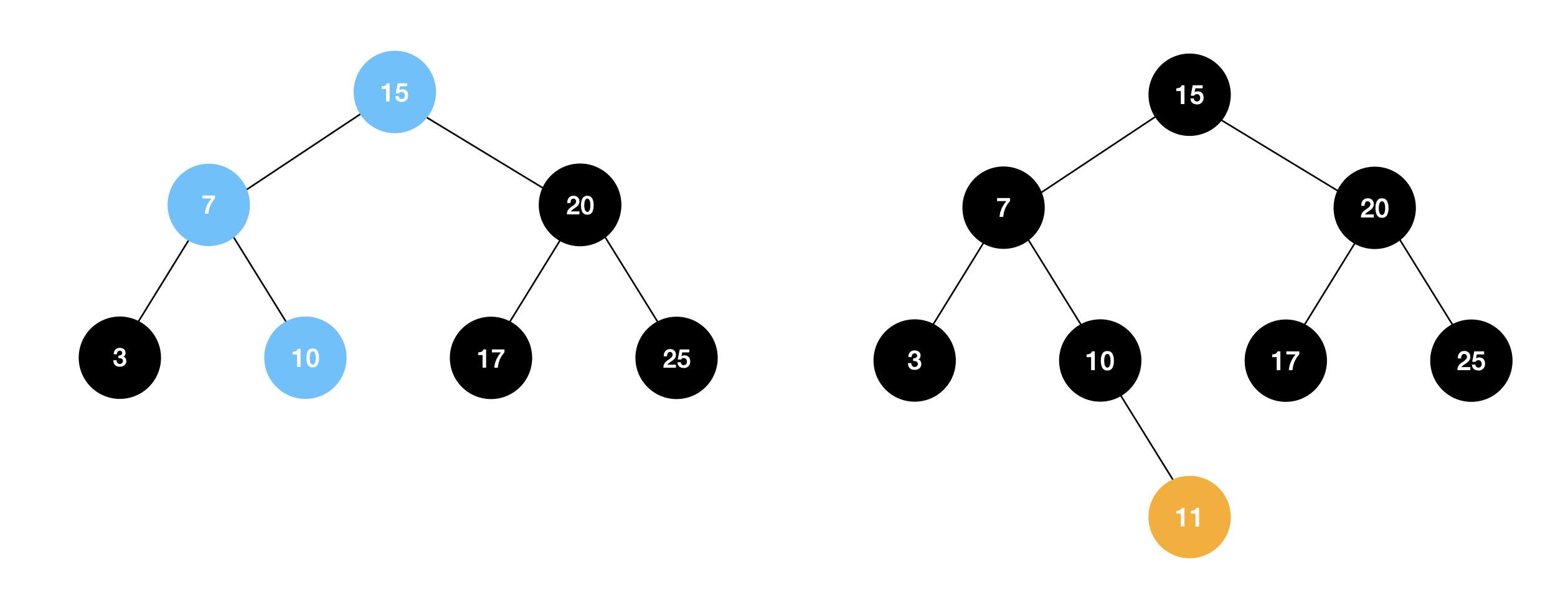
- 루트 노드의 key인 15와 삽입하길 원하는 key인 11을 크기를 비교 (15 > 11)
- 11이 15보다 작기 떄문에 루트 노드의 왼쪽 하위 노드의 키를 비교 (7 > 11)
- 11이 7보다 크기 때문에 노드의 오른쪽 하위 노드의 key와 비교 (10 < 11)
- 11이 10보다 크기 때문에 노드의 오른쪽 하위 노드에 삽입
삭제
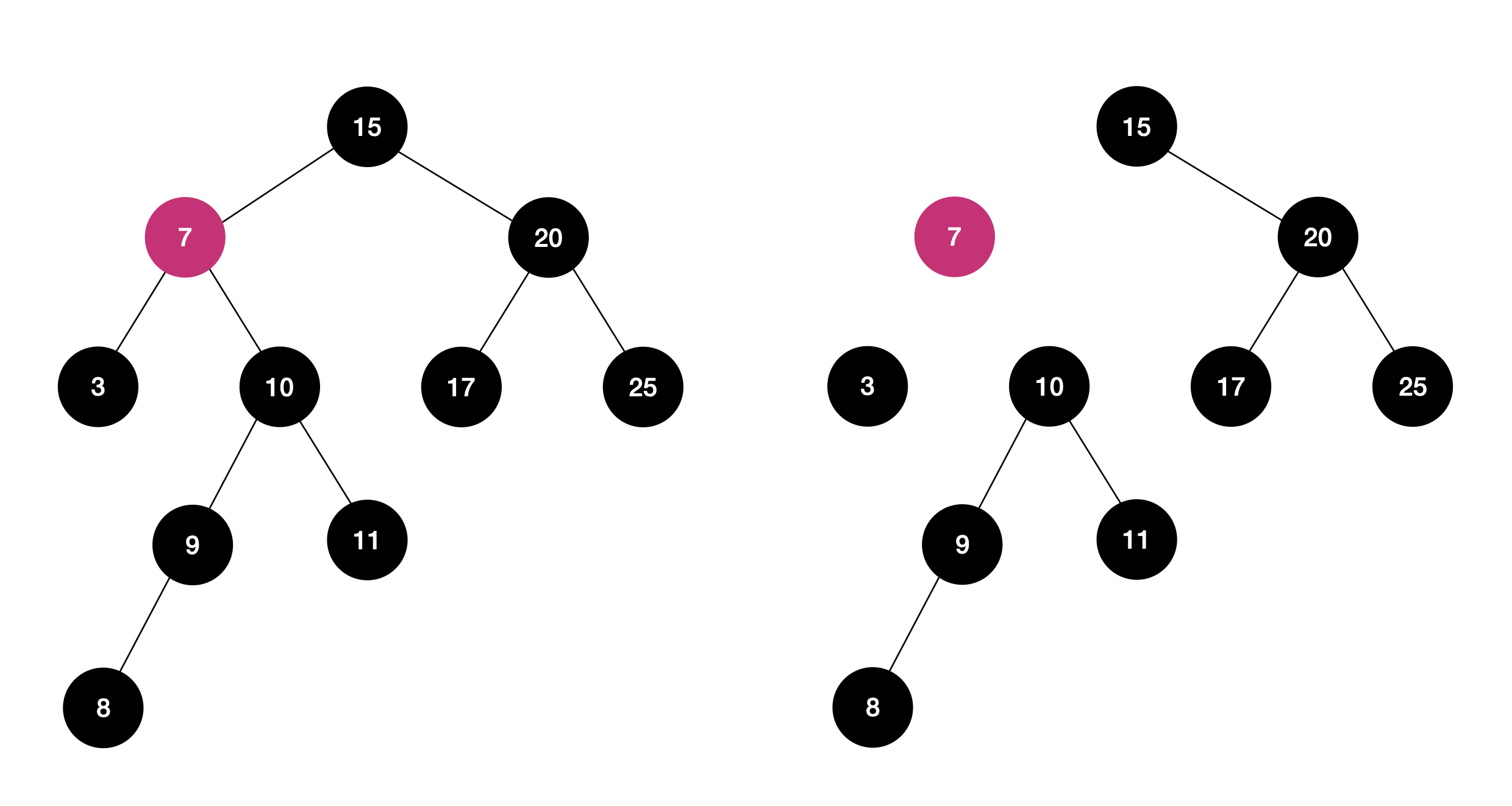
- 삭제를 원하는 노드의 key를 탐색
- 삭제 노드와 연결된 상위 노드와 하위 노드와의 연결을 해제
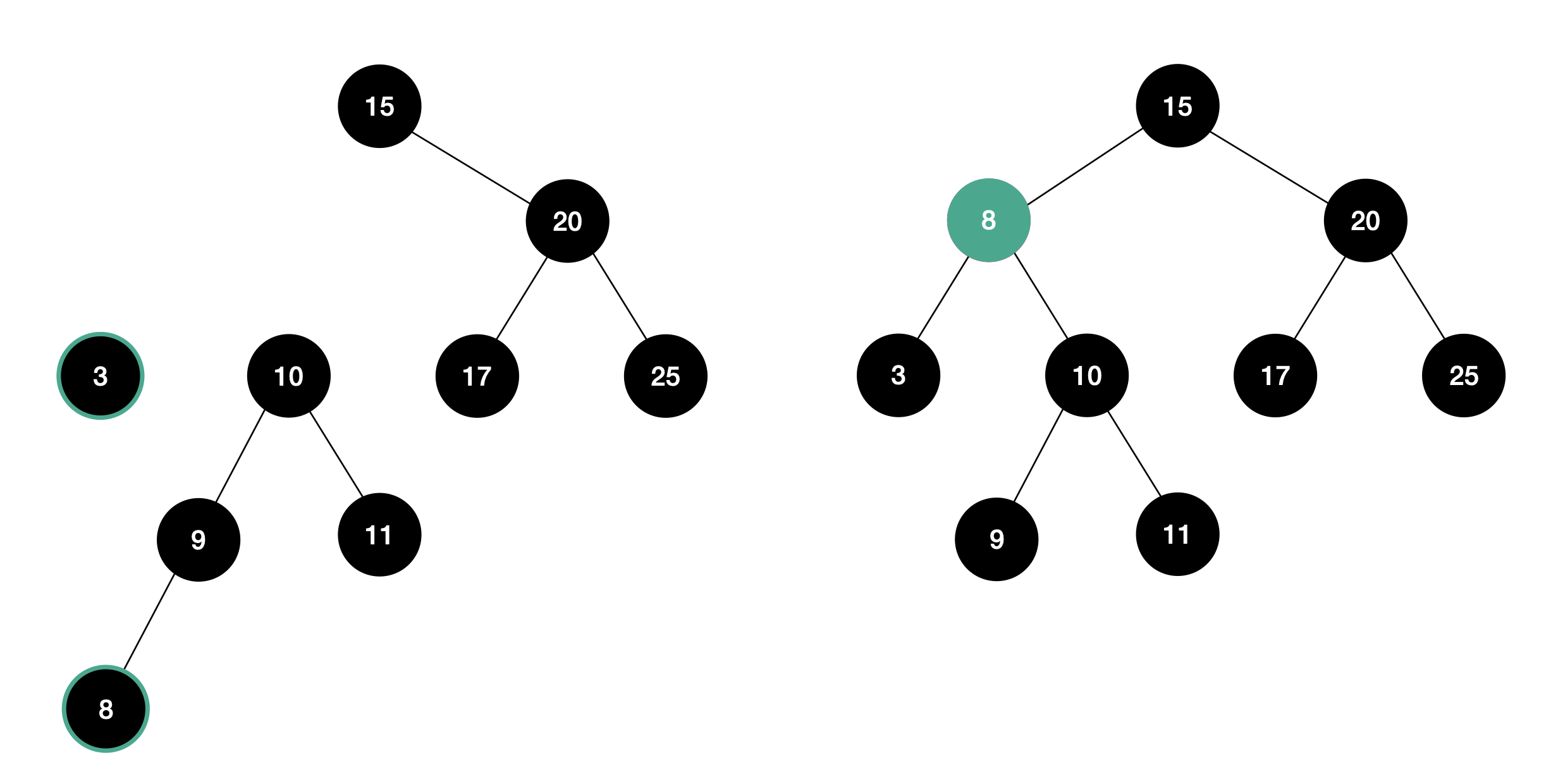
- 메모리에서 노드를 삭제
- 삭제 노드와 대체할 노드를 선택
- 7은 위 트리에서 2번째로 작은 수입니다. 따라서 7이 삭제된다면 이 자리에 1번째로 작은 수인 3과 3번째로 작은 수인 8이 올 수 있습니다. 이 예시에서는 8을 선택하였습니다.
- 대체할 노드는 삭제 노드의 왼쪽 하위 노드의 가장 오른쪽 하위 노드 또는 오른쪽 하위 노드의 가장 왼쪽 하위 노드를 선택하면 됩니다.
- 대체 노드가 삭제 노드를 대체하고 상위 노드와 하위 노드와 연결
- 구현 시 노드의 연결을 해제하고 다시 연결해주는 과정을 생략하고 7과 8인 서로의 key 값 바꾸어 주면 쉽게 구현할 수 있습니다.
구현
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
def in_order_traverse(self, node):
if not node:
return
self.in_order_traverse(node.left)
print(node.value, end=' ')
self.in_order_traverse(node.right)
def insert(self, value):
if self.root:
next_node = self.root
while True:
if next_node.value <= value:
if next_node.right:
next_node = next_node.right
else:
next_node.right = Node(value)
return
elif next_node.value > value:
if next_node.left:
next_node = next_node.left
else:
next_node.left = Node(value)
return
else:
self.root = Node(value)
def search(self, value):
return
def delete(self, value):
if not self.root:
print('삭제할 노드가 없음')
return
curr_node = self.root
delete_node = None
parent_node = None
# 탐색
while True:
if not curr_node:
print('삭제할 노드가 없음')
return
if curr_node.value == value:
delete_node = curr_node
break
elif curr_node.value < value:
parent_node = curr_node
curr_node = curr_node.right
else:
parent_node = curr_node
curr_node = curr_node.left
# 삭제
# delete_node에 하위 노드가 없는 경우
if not delete_node.left and not delete_node.right:
# delete_node가 최상위 노드일 경우
if not parent_node:
self.root = None
# 데이터가 부모 노드의 값보다 클 경우
elif parent_node.value > value:
parent_node.left = None
# 데이터가 부모 노드의 값보다 클 경우
else:
parent_node.right = None
del delete_node
# delete_node에 하위 노드가 존재하는 경우
else:
# 오른쪽 하위 노드가 존재할 경우
if not delete_node.left and delete_node.right:
if not parent_node:
self.root = delete_node.right
elif parent_node.value > value:
parent_node.left = delete_node.right
else:
parent_node.right = delete_node.right
del delete_node
# 왼쪽 하위 노드가 존재할 경우
elif not delete_node.right and delete_node.left:
if not parent_node:
self.root = delete_node.left
elif parent_node.value > value:
parent_node.left = delete_node.left
else:
parent_node.right = delete_node.left
del delete_node
# 둘 다 존재할 경우
else:
change_node = delete_node.right
# delete_node의 자리는 오른쪽 서브 트리의 가장 왼쪽에 있는 하위 노드로 대체함.
# delete_node의 오른쪽 하위 노드의 왼쪽 하위 노드가 없을 경우 그대로 오른쪽 하위 노드가 change_node가 됨.
if not change_node.left:
delete_node.value = change_node.value
delete_node.right = change_node.right
else:
parent_change_node = None
# 대체할 노드를 탐색
while change_node.left:
parent_change_node = change_node
change_node = change_node.left
delete_node.value = change_node.value
parent_change_node.left = change_node.right
del change_node
import random
bst = BinarySearchTree()
nums = []
for i in range(1, 100):
random_num = random.randint(1, 100)
nums.append(random_num)
bst.insert(random_num)
bst.in_order_traverse(bst.root)
print('')
for n in range(len(nums)):
random_num = random.choice(nums)
bst.delete(random_num)
nums.remove(random_num)
bst.in_order_traverse(bst.root)